Kant e la filosofia trascendentale

1. Ci proponiamo in questo saggio di chiarire il senso originario della nozione di trascendentale in Kant, per come Kant stesso l’ha definita. Per questo abbiamo ritenuto di esaminare dettagliatamente la Introduzione alla CRP del 1787, siglata tradizionalmente come versione B. La precedente introduzione del 1781, la versione A, che era un po’ più breve, era divisa in due sezioni che erano titolate in maniera davvero significativa: I. Idea della filosofia trascendentale e II. Suddivisione della filosofia trascendentale. Evidentemente, per Kant, proprio nell’Introduzione doveva essere esposto il nucleo essenziale della sua nozione di trascendentale. Nei titoli dell’edizione del 1787 il termine “trascendentale” non compare più, tuttavia il contenuto della nuova Introduzione non è radicalmente diverso (sebbene ci siano differenze e molte aggiunte). Per qualche ragione, Kant ha scelto di trattare dunque del suo argomento, la filosofia trascendentale, solo nel testo, prescindendo dalle titolazioni e ripartizioni. Alla fine della Introduzione, in entrambe le versioni A e B, Kant fornisce esplicitamente definizione di “trascendentale” che ha in mente.

2. La Introduzione alla CRP del 1787 è composta di sette sezioni numerate, ognuna delle quali possiede un titolo recante una breve sintesi del suo contenuto. La prima sezione si occupa della distinzione tra la conoscenza empirica e la conoscenza pura. Kant ammette subito che la conoscenza comincia sempre con l’esperienza ma insinua anche che non tutte le conoscenze debbano forzatamente sorgere dall’esperienza: «Potrebbe infatti avvenire che la nostra stessa conoscenza empirica sia un composto di ciò che riceviamo mediante le impressioni e di ciò che la nostra facoltà conoscitiva vi aggiunge da sé sola (semplicemente stimolata dalle impressioni sensibili); aggiunta, questa, che non distinguiamo da quella materia primitiva, fintanto che un lungo esercizio non ce ne abbia resi consapevoli, ponendoci in grado di separare i due fattori».[1]

Più chiaro di così. L’ipotesi che viene sostenuta, proprio in apertura, è che la nostra facoltà conoscitiva possieda in sé delle conoscenze non empiriche[2] che essa aggiunge all’esperienza. Kant parla chiaramente di una “aggiunta” di qualcosa da parte della facoltà conoscitiva e dunque di un “composto” come risultato. L’esperienza che noi abbiamo deve dunque esser intesa come un composto di elementi proveniente da fonti diverse. Si tratta inoltre di un’aggiunta della quale non ci rendiamo conto, che non distinguiamo, fintanto che un lungo esercizio non ce ne abbia resi consapevoli, ponendoci in grado di separare i due fattori. L’apporto fornito dalla nostra facoltà conoscitiva al composto non è dunque consapevole (tanto da far presumere che possa avvenire inconsciamente). Tommaso d’Aquino esprimeva esattamente la stessa opinione quando osservava che, a causa della abitudine, non ci accorgiamo dell’ens. Ovviamente, anche Tommaso era proprio sicuro che l’ens ci fosse.[3] C’è un che di iniziatico in queste parole che sarebbe errato sottovalutare. L’esigenza di un “lungo esercizio” per accorgersi di cose di cui nessuno si accorge fa poi venire in mente Husserl e la sua epoché. Oppure la lunga formazione speciale che deve avere l’analista secondo Freud. Qui stanno evidentemente le radici delle filosofie del sospetto.

Kant dunque pone il problema – invero onestamente, anche se la risposta è del tutto prevedibile – se esistano effettivamente siffatte conoscenze a priori. Definendole ulteriormente come conoscenze assolutamente indipendenti da ogni esperienza. Queste conoscenze sono anche definite come pure, tradendo un certo giudizio negativo per quanto è impuro, cioè il lato materiale dell’esperienza. Un altro termine usato da Kant è incondizionato. Risulta chiaro fin dall’inizio, anche se non lo dice esplicitamente, che sono proprio queste le conoscenze che egli definisce come trascendentali e che la filosofia trascendentale è vista da Kant proprio come quell’esercizio analitico, “spirituale”, che ci dovrebbe mettere in grado di separare i due tipi di conoscenza. Procedimento che poi è sempre del tutto analogo alla reductio di Tommaso.

3. Nella seconda sezione Kant abbandona ogni cautela e afferma con decisione che noi siamo senz’altro in possesso di conoscenze a priori, o pure, che entrano nel composto finale della nostra esperienza. Si tratta allora di avere una traccia evidente che ci consenta di individuarle. Che ci consenta di separare il puro dall’impuro. Per Kant (e per noi lettori) è davvero fondamentale il criterio che egli decide di usare per individuare e distinguere quanto vi sia di a priori entro la nostra esperienza. Secondo Kant, i segni sicuri, gli indizi caratteristici di una conoscenza a priori, sono la necessità e la rigorosa universalità. L’affermazione è decisamente apodittica e Kant non spende una parola in più per dimostrare l’assunto. Questo modo categorico di porre la questione è piuttosto imbarazzante, poiché nel dibattito filosofico del tempo era stato evidenziato proprio il fatto che la necessità e l’universalità delle conoscenze umane costituivano un problema. Si trattava del problema per eccellenza di cui stavano discutendo i filosofi più importanti dell’epoca. Dietro, stava il problema ben noto della fondazione, problema dibattutissimo ai tempi di Kant, ma che aveva attraversato tutta la filosofia occidentale.

4. La soluzione “trascendentale” di Kant è dunque già tutta lì: la fondazione dell’esperienza sta in qualcosa di universale e necessario che noi stessi aggiungiamo all’esperienza, per lo più senza accorgercene neanche. Insomma, la necessità e l’universalità stanno in noi. Siamo dunque noi che rendiamo universale e necessaria la nostra stessa esperienza che, altrimenti, non avrebbe alcuna fondazione certa. L’obiettivo di Kant è chiaro fin dall’inizio: fondare la conoscenza in termini universali e necessari. Questo fa parte del suo progetto, di più ampio respiro, di costruire la metafisica come scienza. Chiaramente qui Kant fa a meno di ricorrere a un principio divino, oppure a un intelletto agente, come altri avevano fatto. La conoscenza umana doveva fondarsi su principi universali e necessari collocati nella mente umana.[4] Siamo effettivamente in presenza di una laicizzazione: la mente umana si trova ora ad assolvere a importanti funzioni metafisiche fondazionali che prima erano state riservate a Dio o a qualche suo delegato.

5. Possiamo facilmente intravvedere, dietro alla questione della fondazione della conoscenza posta da Kant, il problema annoso della metafisica di individuare un principio primo, o una serie di principi primi. Un principio perfettamente auto evidente. Un principio che non richieda ulteriore dimostrazione. Non si può non sentire qui l’eco della questione della universalità come l’avevano affrontata gli antichi, ad esempio con i generi sommi, oppure come l’avevano affrontata i medievali attraverso la questione dell’essere necessario. O proprio attraverso il dibattito plurisecolare sui trascendentali.[5]

Kant apparentemente finge di venderci una questione epistemologica e evita di specificare come la sua assunzione circa l’universalità e la necessità delle conoscenze a priori che possediamo e riversiamo nella esperienza sia precisamente una assunzione di carattere metafisico. E sostiene: «Orbene, è facile dimostrare che nella conoscenza umana si dànno effettivamente simili giudizi, necessari e universali nel senso più rigoroso, e quindi puri a priori».[6] Da notare la disinvoltura con cui Kant usa in modo intercambiabile termini come conoscenza, esperienza e giudizio. Ne riparleremo.

6. Vediamole, allora, queste facili dimostrazioni. Le prove portate da Kant sono costituite da “tutte le proposizioni della matematica”, le quali appaiono al senso comune dotate di universalità e necessità. Oppure anche le proposizioni che derivano dalla fisica, come “ogni mutamento deve avere una causa”. Naturalmente, simili argomentazioni potevano apparire assai robuste ai lettori di Kant. Oggi lo sono molto meno.[7] Oppure ancora, Kant sostiene, ahimè, come prova, che queste conoscenze universali e necessarie sono indispensabili per la possibilità dell’esperienza stessa: «Donde mai, infatti, l’esperienza trarrebbe la sua certezza se le regole secondo cui essa procede fossero in ogni caso empiriche, quindi contingenti? Come potrebbero, in questo caso, fungere da princìpi?».[8] Kant qui assume ciò che invece dovrebbe dimostrare e cioè la certezza dell’esperienza. Pur confermando che qui Kant è alla ricerca di principi, l’argomentazione, come ognun vede, è perfettamente circolare. Il mondo empirico è contingente, dunque non può generare nulla che sia universale e necessario. Se abbiamo esperienze che sono (indubitabilmente) universali e necessarie, allora l’universalità e necessità deve provenire da fuori. Gli onesti scolastici medievali erano consapevoli e ponevano esplicitamente la necessità del primo principio, del primo conosciuto, cioè l’ens. E di tutte le sue proprietà trascendentali o fondative.

Tra le “facili” dimostrazioni, Kant propone anche due esperimenti mentali alla Husserl: se dall’esperienza di un corpo si tolgono tutte le proprietà, resterà tuttavia lo spazio; se a un oggetto empirico si tolgono tutte le proprietà esperite resterà pur sempre la nozione della sostanza.[9] Forse simili argomentazioni (che abbondano nella CRP) potevano persuadere i lettori o gli ascoltatori di Kant. Sono comunque tutte argomentazioni ingenue, dubbie o anche del tutto sbagliate.

7. A questo punto, nel terzo paragrafo, data ormai per provata la realtà delle nostre conoscenze a priori universali e necessarie, Kant ipotizza che la filosofia abbia bisogno di una scienza “che determini la possibilità, i principi e l’ambito di tutte le conoscenze a priori”. E questo sarà effettivamente il compito della CRP. Kant continua a suggerire implicitamente (parla di conoscenze) che si tratta di una questione epistemologica. In realtà ha continuato, fin dall’inizio, a giocare sulla ambiguità dei due termini conoscenza e esperienza.[10] Il suo discorso scivola continuamente dalla questione della conoscenza alla questione ontologica o metafisica. Dunque, conclude Kant, la filosofia ha bisogno di una scienza dei trascendentali. Questa nuova scienza, come ognun vede, è perfettamente analoga alla metafisica di Avicenna, a quella di Tommaso, o a quella di Duns Scotus. Si tratta di fondare metafisicamente la possibilità stessa della conoscenza dell’ens e di tutto quel che consegue.

Tuttavia Kant qui avanza un’ulteriore motivazione che senz’altro è di notevole rilievo: una scienza delle conoscenze a priori sarebbe utilissima per saggiare le pretese di conoscenza di discipline che sogliono abbandonare il terreno dell’esperienza. Kant propone qui due esempi. L’esempio in positivo è quello della matematica, la quale può vantare ovunque il suo successo. L’esempio problematico è invece quello della metafisica, che invece faceva continuamente registrare ampi disaccordi e insuccessi. Di qui deriverà il vero e proprio carattere di svolta storica della CRP e cioè il fatto di avere determinato, in termini critici, i limiti delle metafisiche speciali che riguardavano l’Anima, il Mondo e Dio. Insomma, l’apporto storico fondamentale della CRP non sta nella Analitica bensì nella Dialettica trascendentale. Non sarà poco, anche se Kant, proprio su questo punto, sarà perfettamente inascoltato dai suoi successori.

8. Nel quarto paragrafo Kant tratta della distinzione tra giudizi analitici e sintetici. Si tratta qui, nell’intento espositivo di Kant, di produrre una trattazione più formale a proposito della distinzione, già data per scontata, tra puro e empirico e della possibile realizzazione del composto tra i due elementi. Tratta dunque della sintesi a priori. Sono tutti argomenti troppo noti per doverli qui riprendere. Segnalo che gli interpreti di Kant hanno spesso convenuto sulla validità della distinzione tra analitico e sintetico proposta e utilizzata dallo stesso Kant. Recentemente, tuttavia, la validità della distinzione è stata messa in dubbio da W.V.O. Quine, in un suo celebre articolo.[11] Se accogliamo la dimostrazione di Quine, tutto l’impianto della CRP viene invalidato.

9. Nel quinto paragrafo Kant sostiene che “In tutte le scienze teoretiche della ragione sono contenuti, come principi, giudizi sintetici a priori”. Cioè, come si è visto, giudizi che possiedono una componente di conoscenza universale e necessaria a priori o pura. Secondo Kant, i giudizi matematici sono tutti quanti sintetici (e qui spiega diffusamente la sua concezione della matematica). In secondo luogo, afferma che anche “La scienza naturale contiene in sé, come principi, giudizi sintetici a priori”. Anche nella metafisica, almeno secondo quanto intendono i metafisici, devono essere contenute conoscenze sintetiche a priori. Quest’ultima possibilità sarà poi confutata nella Dialettica trascendentale. Matematica, fisica e metafisica dipenderebbero dunque dagli a priori della Ragione.

10. Ci possiamo domandare perché Kant, in questa rassegna, non abbia fatto menzione della logica classica, disciplina che pure conosceva bene, visto che la insegnava. Per Kant la logica classica aveva in sé un elemento di debolezza. Non aveva alcuna autentica fondazione metafisica o trascendentale. Come è noto, la fondazione tradizionale della logica si basava sul principio di non contraddizione (che in Aristotele aveva anche un valore ontologico). Tuttavia, come anche Aristotele sapeva benissimo, il principio era indimostrabile. Doveva essere assunto e basta. Ne derivava che tutti i giudizi logici classici si fondavano su qualcosa che era, in ultimo, indimostrabile. Nel linguaggio di Kant, la logica classica non era ahimè universale e necessaria, era puramente analitica. Dunque, la logica classica, come insieme delle leggi del pensiero, non poteva costituire alcunché, in senso kantiano. La logica classica era semplicemente deduttiva e non trascendentale!

Per questo Kant compie una temeraria innovazione: pone una nuova logica fondata sulla universalità e necessità delle conoscenze a priori. Le quali apparivano a Kant ben più fondate di quelle della logica aristotelica. La logica trascendentale si occuperà così delle conoscenze pure, universali e necessarie, relative alla sensibilità, all’Intelletto e poi anche delle Idee della ragione. Dentro alla esperienza, mescolate con essa, ci sono le conoscenze pure: due intuizioni pure, 12 categorie e l’appercezione. Dunque, nella conoscenza restituita dall’Intelletto – che poi è l’esperienza fenomenica pensata – ci stanno elementi “logici” universali e necessari. Questo significa che l’intelletto è fuso con il mondo, con l’esperienza. L’intelletto costituisce l’intelaiatura logica del mondo. Si tratta dunque – nell’intendimento kantiano – di una logica più profonda di quella aristotelica, capace di regolare non solo il discorso ma di regolare il Mondo dell’esperienza.

11. In Kant si delineano dunque ben due logiche di carattere diverso. Una logica (quella che sarà detta trascendentale) si occupa della costituzione stessa della realtà in modo che questa possa essere conosciuta da noi. Come poi, ad esempio, avverrà massicciamente in Hegel. Questa logica, come ognun comprende, è di fatto una vera e propria ontologia. L’altra logica (quella classica) è una mera tecnica di derivazione dei giudizi. Così la logica tradizionale perde definitivamente il suo carattere fondativo, ontologico, poiché questo è già assolto dalle forme pure universali e necessarie. E diventa semplicemente l’ordine del ragionamento. Solo con George Boole (1815-1864) la logica sarà poi connessa con la matematica.

Questa pretesa kantiana, di una nuova logica che costituisce l’impalcatura della realtà, sta alla base del plurisecolare conflitto sviluppatosi, nella filosofia continentale, tra la cosiddetta logica dialettica e la logica classica. Saranno gli hegeliani e poi ancora i marxisti (e i francofortesi) a sviluppare il filone della logica dialettica e a contrapporlo alla logica classica, considerata una logica di tipo inferiore, legata a un meccanicismo strumentale e scientista. Ancora un pur grande filosofo italiano come Galvano della Volpe poteva sognare che la dialettica hegelo marxiana potesse divenire la “logica delle scienze sociali”.

12. Nel sesto paragrafo, Kant si occupa del problema generale della ragion pura. E cioè di come siano possibili i giudizi sintetici a priori. Segue la discussione di una serie di altri problemi ivi impliciti, che qui, per i nostri scopi, possiamo tralasciare. Finalmente abbiamo il settimo paragrafo, quello conclusivo, dove compare esplicitamente, nel corpo testuale, anche il termine “trascendentale”. Il titolo tuttavia è Idea e partizione di una scienza speciale, denominata Critica della ragion pura. Così Kant ne spiega l’esigenza: «Infatti la ragione è la facoltà che ci dà i princìpi della conoscenza a priori. Ragion pura è quindi quella che contiene i princìpi per conoscere qualcosa prettamente a priori. Un organo della ragion pura sarebbe un insieme di quei princìpi in base ai quali tutte le conoscenze pure a priori possono essere acquisite ed effettivamente poste in atto. L’applicazione totale d’un tale organo costituirebbe un sistema della ragion pura. Ma poiché questo sistema, pur essendo assai richiesto, lascia ancora aperta la questione se anche qui, ed in quali casi, una estensione in generale della nostra conoscenza sia possibile, possiamo allora considerare una scienza della semplice valutazione della ragion pura, delle sue sorgenti e dei suoi limiti, come la propedeutica al sistema della ragion pura. Una scienza siffatta non dovrebbe chiamarsi dottrina, ma soltanto critica della ragion pura; e, rispetto alla speculazione, la sua utilità sarebbe in realtà solo negativa, poiché servirebbe, anziché all’allargamento, alla semplice purificazione della nostra ragione, liberandola dagli errori; il che è di già un grandissimo guadagno».[12]

Quando parla di “organo” Kant ha ovviamente in mente l’organon aristotelico. E ha senz’altro in mente che la sua filosofia trascendentale si appresterebbe a costituire un nuovo organo, destinato a soppiantare l’organo aristotelico. C’è qui un accostamento repentino delle conoscenze a priori, che noi mescoliamo ad altro per generare la nostra esperienza, a un concetto come quello di Ragione.[13] Si noti la definizione di Ragion pura che qui è implicita: essa ci fornisce i principi della conoscenza a priori, dunque la ragione entra nella costituzione stessa della nostra esperienza, nella costituzione di ciò che Kant chiamerà fenomeno. Il fenomeno è fatto di Ragione mescolata ad altro. La Ragione produttrice e depositaria di a priori non è più la semplice ragione discorsiva che calcola le argomentazioni, è bensì una entità che entra direttamente nella costituzione del Mondo esperito. Una specie di Dio minore creatore che sta – non si sa come – nella testa dell’uomo. Un intelletto agente di arcaica memoria. La ragione con le sue conoscenze a priori costituisce effettivamente la intelaiatura di tutto quel che c’è di esperibile. Si apre la porta qui alla prospettiva hegeliana per cui la Ragione costituisce la realtà stessa (= idealismo). Il mondo è razionale perché fatto di ragione. Volendo si può risalire indietro fino ad Avicenna (980-1037).

13. A questo punto (siamo giunti ormai a metà del par. VII, l’ultimo) Kant spiega esplicitamente cosa intenda con la nozione di trascendentale. «Chiamo trascendentale ogni conoscenza che si occupi, in generale, non tanto di oggetti quanto del nostro modo di conoscere gli oggetti nella misura in cui questo deve essere possibile a priori. Un sistema di tali concetti potrebbe esser detto filosofia trascendentale».[14] La filosofia trascendentale, nell’intento di Kant, si occupa dunque dei principi a priori che rendono possibile la costituzione della realtà e, dunque, anche la sua conoscenza. La realtà fenomenica per Kant è costituita in quanto vien conosciuta. Ma la costituzione deve precedere la conoscenza. La filosofia trascendentale si occupa in altri termini esattamente di ciò che i medievali chiamavano transcendentalia. Solo “nella misura in cui” questi sussistano effettivamente. Ma Kant ha già mostrato che sussistono. Senza i principi a priori della Ragione, niente filosofia trascendentale. Ma anche niente esperienza. Niente realtà fenomenica. La filosofia trascendentale è dunque strettamente legata alla sintesi a priori. Infatti la domanda fondamentale cui tenterà di rispondere la CRP è proprio come questa sia possibile. Per i medievali, i transcendentalia erano le proprietà profonde della creazione divina, i principi primi che costituivano l’ens creato e lo rendevano intelligibile. La filosofia trascendentale medievale era l’erede della filosofia prima, la scienza dell’ente in quanto ente. Ora, in Kant, la filosofia trascendentale è la scienza dei principi primi a priori grazie ai quali la Ragione costituisce il mondo.

14. Nel proseguimento della CRP Kant userà spesso il termine trascendentale (anche se con sfumature di significato talvolta piuttosto diverse)[15] senza più fornire alcuna ulteriore spiegazione, presupponendo evidentemente che al suo lettore sia bastata la definizione fornita nella introduzione. Tuttavia a un certo punto ritornerà esplicitamente sulla questione. Nella Logica trascendentale, dopo avere presentato la tavola delle sue nuove categorie, ricavate anche ma non solo dalle categorie aristoteliche, quasi come per prevenire l’obiezione di avere trascurato qualcosa, Kant afferma quanto segue: «Nella filosofia trascendentale degli antichi si trova però ancora un capitolo comprendente concetti puri dell’intelletto, i quali, pur non rientrando nell’elenco delle categorie, dovevano tuttavia valere come concetti a priori degli oggetti; ma in effetti essi accrescerebbero in tal modo il numero delle categorie, il che non è possibile».[16]

Si noti che qui Kant chiama concetti puri dell’intelletto proprio i trascendentali medievali. Cioè concetti che non sono ricavati dalla esperienza ma che sussistono di per sé dentro l’Intelletto. Avrebbe anche potuto dire a priori. Più chiaro di così! Pur essendo il loro elenco variato assai nel corso della storia filosofica, Kant, proseguendo, si limita a citarne solo tre: «Essi sono racchiusi nella proposizione tanto celebre presso gli scolastici: quodlibet ens est Unum, Verum, Bonum. Benché l’uso di questo principio, a giudicare dalle conseguenze (che altro non produssero se non proposizioni manifestamente tautologiche), abbia avuto un risultato miserevole al punto che ai nostri tempi la metafisica suole farne menzione quasi solo per deferenza – tuttavia un pensiero che ha resistito così a lungo, per vuoto che sembri, è pur sempre degno di un’indagine circa la sua origine e rende lecita la supposizione che trovi il suo fondamento in qualche regola dell’intelletto, sottoposta, come spesso accade, a una falsa interpretazione».[17] Insomma, Kant s’interroga circa la persistenza della tematica dei trascendentali nel corso della storia della metafisica occidentale e sospetta che, dietro a questa persistenza, possa esserci eventualmente qualcosa. La tavola, peraltro assai mutevole, dei vecchi trascendentali non collimava senz’altro con la sua, appena presentata.

15. Kant così svela esplicitamente al lettore quale sia l’arcano che sta dietro alla terminologia dei trascendentali, sostenendo che i veri trascendentali sono i suoi, quelli che ha appena finito di elencare e che i trascendentali degli antichi erano dovuti a una prospettiva errata. La prospettiva errata consisteva nel fatto che i trascendentali erano stati considerati anche come proprietà delle cose e non soltanto della mente. Spiega così che: «Questi presunti predicati trascendentali delle cose altro non sono che esigenze e criteri logici di ogni conoscenza delle cose in generale, a fondamento della quale essi pongono le categorie della quantità che sono: unità, pluralità e totalità. Ma queste categorie, che avrebbero dovuto esser prese effettivamente in senso materiale, come proprie della possibilità delle cose stesse, gli antichi le assunsero in effetti soltanto nel significato formale, come proprie dell’esigenza logica relativa ad ogni conoscenza, tuttavia considerando incautamente questi criteri del pensiero come proprietà delle cose stesse».[18]

La argomentazione kantiana è decisamente un poco contorta. Ho messo in nota anche la traduzione di Esposito. Comunque il senso è abbastanza chiaro. L’errore degli antichi sarebbe consistito nel negare il carattere esclusivamente mentale/ formale dei trascendentali e soprattutto nel negare il loro carattere costitutivo dell’esperienza. Secondo Kant i tre principali trascendentali degli antichi sarebbero riconducibili alle sue nuove categorie della quantità, che invece hanno carattere mentale e costitutivo. Gli antichi invece considerarono i trascendentali sia come entità logiche (pertinenti l’intelletto) sia come entità ontologiche (pertinenti tutte le cose). Questo poiché essi condividevano (stupidamente, dal punto di vista di Kant) una teoria della verità come corrispondenza. Per Kant, dopo la sua “rivoluzione copernicana”, la teoria della verità come corrispondenza vale solo dentro il fenomeno. La verità non può che rispecchiare circolarmente ciò che la mente ha già a priori dentro di sé e che ha appena messo nel fenomeno.

16. Insomma, per Kant l’erronea dottrina medievale dei trascendentali sarebbe derivata dal fatto che i medievali non conoscevano ancora la filosofia di Kant, e quindi finirono per collocare oggettivasmente nelle cose quelli che invece per Kant sono soltanto dei criteri della conoscenza, degli a priori della Ragione. In effetti, nel seguito del testo citato, Kant ritiene di mostrare come i tre trascendentali che ha riportato possano essere facilmente ricondotti alle categorie della quantità, nella nuova tavola delle categorie che egli ha appena presentato.

Kant può permettersi di far questo perché – dopo la sua “rivoluzione copernicana” – non ha più bisogno di un qualche diverso fondamento dell’ens. Il fondamento c’è già. Le categorie kantiane hanno già preso il posto dell’ens (e dei suoi modi) e ora, dalla loro collocazione come a priori, possono svolgere la vecchia funzione fondazionale dei trascendentali medievali (motivo per cui il loro nome è rimasto ed è stato addirittura valorizzato). La preoccupazione di Kant, che aveva appena finito di ricavare i concetti puri dell’intelletto dalla tavola dei giudizi della logica tradizionale, era quella di rassicurare che il suo elenco fosse completo e che non fosse il caso di aggiungere, come ulteriori concetti puri, qualcuno dei trascendentali medievali.

17. Considerando il rapporto tra i trascendentali kantiani e quelli medievali possiamo accorgerci – oltre a una loro sostanziale analogia – di un fatto abbastanza sorprendente ma non troppo: quello che Kant presenta al suo lettore è esattamente uno scivolamento delle categorie tradizionali dentro i transcendentalia. 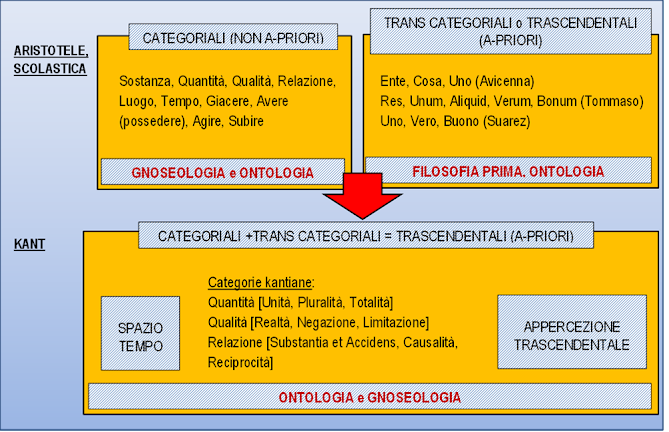Kant provvederà cioè a mescolare nelle sue forme a priori entità che nella filosofia scolastica precedente erano state accuratamente tenute distinte. Nella fig. 1, in appendice, abbiamo realizzato una rappresentazione grafica della situazione. I trascendentali medievali erano transcategoriali (situati cioè al di là delle categorie) e svolgevano un compito opposto a quello delle categorie. Mentre le categorie presiedevano alla distinzione, servivano cioè per descrivere la varietà del mondo sensibile, i trascendentali identificavano invece i caratteri comuni dell’ens, erano perciò il presupposto di qualsiasi conoscenza (ed erano a-priori, posti dentro a tutte le cose!). Visto con gli occhi del medioevo e della Scolastica, il procedimento kantiano doveva apparire estremamente familiare, seppure alquanto velleitario. Dietro al problema della sintesi a priori gli scolastici non potevano non scorgere ancora il vecchio problema della metafisica: di connettere le conoscenze provenienti dal mondo sensibile, attraverso i sensi, con una serie di conoscenze a priori (considerate cioè come non derivanti dalla esperienza, i trascendentali, appunto). Il problema era sempre quello di cui già si trattava nel De anima aristotelico: come l’intelletto potesse cogliere la forma intelligibile presente nelle cose.[19] Il problema era passato, nel neoplatonismo e poi in Avicenna. E poi via di seguito, fino a Suarez e poi ai metafisici del Seicento e del Settecento.

18. Il progetto kantiano doveva apparire velleitario perché se c’era qualcosa che era sempre rimasto fermo nella lunga storia dei transcendentalia era la distinzione rigorosa tra i trascendentali da una parte e le categorie aristoteliche dall’altra. I trascendentali, anche nel nome, non erano categorie, non potevano essere categorie, proprio perché, per svolgere il loro compito, andavano necessariamente oltre le categorie! I trascendentali avevano il compito fondazionale, svolgevano un ruolo fondativo della filosofia prima, della metafisica elementare (metaphysica generalis). Dal punto di vista degli scolastici, si trattava dunque di mettere i transcendentalia della metphysica generalis (quale che fosse effettivamente il loro elenco) a fondamento primo a priori dell’uso delle categorie aristoteliche, le quali tuttavia mantennero sempre la loro autonomia, non furono mai contestate perché presiedevano ad assicurare la conoscenza umana del mondo e rispecchiavano l’ordine del mondo sensibile. Per Aristotele poi, nessuna sostanza poteva essere conosciuta a priori.[20] Per lui la sostanza prima era il sinolo! La ricerca dei principi a priori era stata introdotta in seguito alla platonizzazione di Aristotele e al suo adattamento al pensiero cristiano. Kant, come s’è visto, ha cercato di fare sostanzialmente la stessa cosa degli scolastici. Con un piccolo grande problema. Vogliamo chiamalo errore? O vogliamo chiamarlo fallacia, come fa Maurizio Ferraris?[21]

19. La fallacia fondamentale sta in questo: Kant nella CRP – nella Estetica trascendentale e nella Analitica trascendentale – ha messo anche le categorie (alcune tra quelle più importanti) dentro i transcendentalia. Così lo spazio e il tempo (ma anche la qualità, la quantità, la sostanza, e altro ancora, come la causalità che – si noti bene – per Aristotele non era affatto una categoria), che erano le forme volte alla conoscenza del mondo sensibile e non alla metafisica, diventano ora conoscenze a priori universali e necessarie. Un pasticcio davvero ragguardevole. Ciò significherà considerare le proprietà fondamentali delle cose del mondo come degli a priori metafisici residenti nell’Intelletto. Il risultato sarà, com’è noto, la mentalizzazione del Mondo. Il mondo così diventerà compiutamente mind dependent. Questa scelta, come è noto, darà vita alla prospettiva dell’idealismo trascendentale. E a tutte le successive filosofie “trascendentali” dell’Ottocento e del Novecento.

20. È facile oggi comprendere, per noi, come, da questa fallacia trascendentale, siano derivati i tratti fondamentali della filosofia continentale, nei due secoli successivi e più. Dopo Kant, i filosofi continentali (tranne pochi) non dubiteranno più che ci siano degli a priori. E, soprattutto, non faranno altro che continuare a domandarsi, seppure in modalità assai diverse, quali siano i veri a priori (sulla base di ciò che, di volta in volta, sarà ritenuto, più o meno arbitrariamente, come universale e necessario o, se si vuole, fondativo). Quali siano cioè, ancora, i veri transcendentalia che costituiscono il mondo. In proposito, dopo avere violato, grazie a Kant, i confini tra metafisica fondazionale e fisica del mondo naturale, poteva venir fuori qualsiasi cosa. L’elenco di supposti trascendentali che sono stati mescolati col mondo entro improbabili sintesi a priori è davvero lungo, e ancora in continua crescita. Ne riporto qui un elenco esemplificativo: l’Io, l’Idea, lo Spirito, l’essere, la volontà, la vita, la libertà, la volontà di potenza, la storia, la struttura, la materia economico sociale, l’alienazione, la merce, l’ego trascendentale, il testo o la testualità, il potere, il linguaggio, l’interpretazione, l’esistenza, il nulla, la tecnica, il desiderio, la libido, l’inconscio, la ragione strumentale. Si noti anche che alcune filosofie continentali, resesi forse conto della sterilità delle loro pratiche, non hanno trovato di meglio che vivere di rendita, raccontando e celebrando proprio la annunciata sparizione dell’a priori dal mondo. Così abbiamo avuto la fine della verità, la fine del soggetto, la fine della storia, l’eclissi della ragione, la morte di Dio, la sparizione dell’Essere, la fine della metafisica, la morte dell’Occidente e quant’altro. Una sorta di nichilistico lutto permanente in memoria della scolastica kantiana perduta.

 

APPENDICE

Fig.1 – Lo scivolamento progressivo dei categoriali aristotelici nei trascendentali kantiani.

 

Giuseppe Rinaldi (30/06/2025)

 

OPERE CITATE

2012 Aertsen, Jan A., Medieval Philosophy as Transcendental Thought. From Philip the Chancellor (ca. 1225) to Francisco Suárez, Brill, Leiden.

1966 Aristotele, Anima (A cura di Giancarlo Movia), Rusconi Libri, Milano.

2001 Ferraris, Maurizio, Il mondo esterno, Bompiani, Milano.

2004 Ferraris, Maurizio, Goodbye Kant! Cosa resta oggi della Critica della ragion pura, Bompiani, Milano.

2014 Kant, Immanuel, Critica della ragion pratica e altri scritti morali (A cura di Pietro Chiodi), UTET, Torino. [1787]

2004 Kant, Immanuel, Critica della ragion pura (A cura di Costantino Esposito), Bompiani, Milano. [1781/ 1787]

1992 Kemp Smith, Norman, Commentary to Kant’s “Critique of Pure Reason”, Humanities Press International Inc,, Atlantic Highlands, NJ. [1918- 1923]

1953 Quine, Willard van Orman, From a Logical Point of View. Nine logico-Philosophical Essays, Harvard University Press, Cambridge. Tr. it.: Da un punto di vista logico. Saggi logico-filosofici, Raffaello Cortina Editore, Milano, 2004.

 

NOTE

 [1] Cfr. B2. In questo commento, a meno di altra segnalazione, seguo la traduzione di Chiodi.

[2] Non empiriche non vuol dire necessariamente innate. Ogni specie di uccelli sa come fare il nido, ma questa non è una conoscenza a priori nel senso di Kant. La non empiricità per Kant è una nozione metafisica che ha a che fare con la Ragione.

[3] Questo atteggiamento, di postulare l’esistenza necessaria di cose di cui nessuno si accorge, è tipica della visione trascendentale.

[4] Sottolineo che oggi la semantica di “mente” non corrisponde a ciò che intendeva Kant. Nei suoi scritti latini aveva usato animus. Solitamente usa il termine Gemüt. In Italiano è stato tradotto anche come Spirito da Gentile e Lombardo - Radice. Mente porta con sé una connotazione cognitivista che è assolutamente estranea a Kant.

[5] Su questo punto si veda Aertsen 2012.

[6] Cfr. B4.

[7] Il dibattito circa i fondamenti della matematica è oggi quanto mai aperto. E la maggioranza degli studiosi non sembra concordare con Kant.

[8] Cfr. B5.

[9] Qui Kant fa un uso comune dei termini spazio e sostanza ed evita ogni definizione rigorosa. Sull’uso allegro che Kant fa di queste nozioni si veda il mio saggio Finestre rotte: La chiocciola di Kant e altre storie spaziali.

[10] Su questa ambiguità ha recentemente insistito Maurizio Ferraris. Cfr. Ferraris 2001 e la questione della ciabatta.

[11] Cfr. Quine 1953. L’articolo in questione è titolato Due dogmi dell’empirismo.

[12] Cfr. B25.

[13] In questa fase introduttiva Kant, comprensibilmente, non distingue ancora tra Intelletto e Ragione.

[14] Cfr. B25.

[15] Sui diversi usi kantiani di “trascendentale” si veda Kemp-Smith 1992.

[16] Kant, CRP, B113 e segg.

[17] Kant, CRP, B113 e segg.

[18] Kant, CRP, B114 e segg. Traduzione Chiodi. La resa nelle traduzioni disponibili in italiano è piuttosto contorta. Riporto la traduzione di Esposito: «Questi presunti predicati trascendentali delle cose, non sono altro che delle esigenze e dei criteri logici di ogni conoscenza delle cose in generale, e pongono a fondamento di questa conoscenza le categorie della quantità, vale a dire l’unità, la pluralità e la totalità. Sennonché, queste categorie, che avrebbero dovuto essere intese in senso propriamente materiale, e cioè come appartenenti alla possibilità delle cose stesse, in realtà furono intese dagli antichi soltanto in senso formale, come appartenenti all’esigenza logica che riguarda ogni conoscenza, sebbene poi essi trasformarono incautamente questi criteri del pensiero in proprietà delle cose in se stesse».

[19] Cfr. De Anima, III, 4 e III, 5.

[20] A meno che non si voglia invocare qui l’intelletto potenziale. Il quale potrebbe avere dentro di sé, in potenza, qualsiasi cosa, ma se resta in potenza e non si attua è come se non ci fosse. A dire il vero, la teoria dell’intelletto contenuta nel De Anima non è tra le più chiare.

[21] Cfr. Ferraris 2004.

 

 

 

 

 

. 

Referendum 2025

1. L’8 e 9 giugno 2025 si sono tenuti, nel nostro Paese, i Referendum sul lavoro e la cittadinanza.[1] Quattro Referendum riguardanti il lavoro erano stati proposti dalla CGIL e uno, quello sulla Cittadinanza, era stato proposto da Più Europa. È noto che un’altra proposta di Referendum, quella sull’Autonomia differenziata, non era stata accolta dalla Corte costituzionale. Nessuno dei referendum ha raggiunto il quorum necessario per la validità. Il numero dei votanti si è attestato intorno al 30,58% degli aventi diritto. Subito dopo è iniziata la sarabanda delle interpretazioni. La sconfitta dei Referendum ha prodotto l’esultanza di coloro che si erano pronunciati per il No o che avevano fatto propaganda per l’astensione. Da parte dei sostenitori del Sì ci sono stati ampi tentativi per mostrare come anche il risultato negativo non era poi così negativo. I commenti circa i risultati tuttavia non si sono allontanati più di tanto dalle considerazioni da dopo partita, su chi ha vinto e chi ha perso, chi ha segnato e chi no.

2. Ci si poteva attendere come risultato collaterale, indipendentemente dall’esito positivo o meno, un generale approfondimento circa le questioni riguardanti la condizione del lavoro nel nostro Paese o sulla questione della cittadinanza. Soprattutto nel campo della sinistra, il campo politico che ha promosso i Referendum, ci si poteva attendere, come risultato secondario, l’elaborazione di idee per una proposta organica di riforma sulle questioni del lavoro, una specie di nuovo Statuto dei lavoratori, oppure una altrettanto organica proposta di riforma sulle questioni della cittadinanza e dei migranti. Il risultato invece è stato una focalizzazione su singole minuzie, peraltro assai tecniche, e una distrazione dalle questioni politiche fondamentali. Forse l’impresa di un progetto organico di riforma su lavoro e cittadinanza è una questione che va oltre le capacità dei soggetti coinvolti. Invece le divisioni e le incomprensioni sono rimaste, e forse si sono anche aggravate. In altri termini, non si è andati gran che oltre al tifo per le diverse squadre.

In questo saggio cercherò di mettere in ordine alcune riflessioni circa quanto è avvenuto, sulle cause e sulle conseguenze di questo evento, che costituisce senz’altro un importante elemento di svolta proprio sulle questioni riguardanti il lavoro e la cittadinanza nel nostro Paese.

3. Possiamo anzitutto fare un ragionamento sugli antecedenti istituzionali. Val la pena, cioè, di fare qualche considerazione generale sui Referendum in Italia. Quando i Referendum erano stati pensati, il quorum era l’ultimo dei problemi. Le percentuali dei votanti alle elezioni in genere erano altissime. Alle ultime elezioni politiche del 2022, invece, l’affluenza in Italia (senza considerare i votanti all’estero) alla Camera si è attestata al 63,91% (29 475 383) su un corpo elettorale di 46 120 143. Gli astenuti dunque ammontavano al 36,09% (16 644 760). Questa attuale situazione della partecipazione elettorale nel nostro Paese significa che la competizione tra chi propone un Referendum e chi lo rifiuta e/o si astiene è di estrema disparità. I No, senza far proprio niente, partono mediamente con il vantaggio di un terzo. Per superare il quorum, occorre, dunque, che i referendum siano altamente attrattivi.

4. Il corpo elettorale per i 5 quesiti referendari era di 51 301 377 elettori, di cui 45 997 941 in Italia (registrati in 61 591 sezioni) e 5 303 436 all’estero (registrati in 1 863 circoscrizioni consolari).[2] Dunque il quorum, riguardante l’Italia più estero, avrebbe dovuto essere di 25 650 689. Proviamo ora a fare un esercizio teorico, domandandoci quanti dei votanti abituali dovremmo coinvolgere per riuscire a raggiungere questo quorum. Se usiamo come indicatore di astensionismo il tasso di astensione alla Camera del 2022 e cioè il 36,09% e lo applichiamo al corpo elettorale del referendum avremo una aspettativa di astensione di 18 514 667. E un corpo di ipotetici votanti effettivi di 32 786 710. Poiché il quorum è fissato in 25 650 689, allora, per ottenere il quorum, si sarebbe dovuto portare a votare il 78% di coloro che di solito vanno a votare. Quasi l’80%! Il calcolo qui presentato ovviamente è puramente teorico, ma dovrebbe far capire la difficoltà a raggiungere il quorum in un’epoca in cui l’astensionismo standard si attesta a un terzo del corpo elettorale.

Certo, si può pensare che il Referendum possa pescare tra gli astenuti, ma potrebbe anche ugualmente allontanare un contingente dei votanti abituali. Si tratta di fenomeni non univoci e decisamente poco prevedibili. Secondo Wikipedia, “Dal 1946 a oggi in Italia si sono svolti 83 referendum nazionali, di cui 77 referendum abrogativi, un referendum istituzionale, un referendum di indirizzo e quattro referendum costituzionali”. Tra i 77 referendum abrogativi, dunque 38 non hanno raggiunto il quorum. In pratica la metà. Come tirare a testa o croce.

5. Tutto questo significa che i due promotori dei Referendum (la CGIL e Più Europa), solo considerando la natura intrinseca dell’istituto referendario, si sono assunti un rischio molto alto di insuccesso. A queste argomentazioni si obietta solitamente che se la Corte avesse ammesso il Referendum sulla Autonomia differenziata, questo avrebbe fatto da elemento trainante, tanto da far raggiungere il quorum con buona probabilità. Forse questo ragionamento ha qualche fondamento. Questa argomentazione tuttavia non fa molto onore a chi la propone e sa di espediente furbesco. Ci sarebbero allora due tipi di Referendum, quelli che interessano davvero il pubblico (quelli sicuri) e quelli che già in partenza si presume che non siano granché attrattivi. Mettere dei referendum considerati in partenza poco attrattivi in coda a quelli sicuri, pensando di sfruttare l’effetto scia, getta un’ombra sul merito stesso dei quesiti e sulle buone intenzioni dei proponenti.

6. Va poi considerato che il Referendum abrogativo è un istituto per sua natura alquanto delicato e andrebbe usato con ogni cautela. Dovrebbe vertere su grandi questioni, di interesse davvero generale, che implichino un Sì o un No, chiaro e distinto. Non dovrebbe essere usato come sostituzione della legislazione corrente e, soprattutto, con riferimento a tecnicalità poco comprensibili alla maggior parte degli elettori. La stessa natura abrogativa dello strumento fa sì che spesso si proceda con la soppressione di “pezzi” di leggi (aggettivi, commi, articoli) che comunque rendono monco un dispositivo giuridico che abbia comunque avuto una sua qualche organicità all’origine. Leggi monche non è detto che diventino ipso facto delle buone leggi. Ad esempio, nel caso della Cittadinanza, che è questione oltremodo complessa, la semplice riduzione temporale da dieci a cinque anni per ottenere la cittadinanza, è una soluzione monca, che può magari avere anche un nobile valore simbolico, ma che non entra neppure nel merito effettivo delle questioni coinvolte. E non garantisce l’efficacia della soluzione derivante.

7. Era prevedibile la sconfitta? Soprattutto, era prevedibile una sconfitta di queste proporzioni? Abbiamo già considerato la difficoltà in sé a raggiungere il quorum in un’epoca nella quale l’astensione elettorale media vale più di un terzo degli elettori. Tuttavia si poteva ben fare qualche sondaggio empirico preventivo. È appena il caso di considerare che ormai siamo dotati di notevoli strumenti per indagare gli orientamenti della opinione pubblica. Un banale sondaggio – se fatto bene – con un campione tra 2000 e 5000 soggetti può fotografare gli orientamenti della opinione pubblica e prevedere gli esiti di una consultazione con margini di errori minimi, dal più o meno 4% fino al 1,5%. Un sondaggio ben fatto, dal costo irrisorio rispetto ai costi materiali e politici di un referendum perso, avrebbe potuto consigliare circa l’opportunità di procedere o di desistere. Avrebbe permesso di quantificare il rischio. La presunzione di conoscere direttamente il mondo sociale è un brutto vizio, che viene da lontano. Soprattutto da chi è abituato a investirsi della rappresentanza del mondo sociale, senza darsi però la pena di consultare il mondo sociale stesso. Il sindacato (la CGIL) si vanta di navigare nel sociale, come “un pesce nell’acqua”, ma poi si dimostra incapace di usare gli strumenti di conoscenza del mondo sociale che abbiamo a disposizione. Aggiungo che, nella tradizione culturale della CGIL, il motivo dell’uso delle scienze sociali è stato ben presente e ha dato risultati consistenti. Basti ricordare la rigorosa rivista Inchiesta, diretta da Vittorio Capecchi o i gloriosi Quaderni di Rassegna sindacale. Sarebbe utile anche dare un’occhiata alla rivista I Consigli della soppressa FLM.

8. Proviamo però ora a entrare nel merito dei quesiti posti. Se consideriamo anche il Referendum sull’Autonomia differenziata che è stato cassato dalla Corte, si trattava indubbiamente di quesiti che andavano contro l’operato del Governo della attuale maggioranza, ma anche contro l’operato di governi precedenti (nella fattispecie il governo Renzi). Due dei Referendum sul lavoro si riferivano a norme varate dal governo Renzi. Sul piano formale è del tutto legittimo che forze varie di opposizione (partiti, sindacati, alcune Regioni dissidenti dal governo) usino i referendum per contestare i provvedimenti della maggioranza o di governi precedenti. Il Referendum è a pieno titolo un’istituzione di carattere politico. Tuttavia occorre che i quesiti siano considerati rilevanti non solo per chi li propone ma anche per l’opinione pubblica degli elettori che li riceve.

9. Dirò poche cose sul Referendum sulla Cittadinanza. Nasce probabilmente da un’oggettiva debolezza dell’attuale opposizione sulla questione dei migranti. Si tratta di una delle questioni più divisive all’interno dell’opposizione, la quale, nella legislatura precedente, essendo in maggioranza, non era riuscita neanche a promuovere una legge per dare la cittadinanza ai nati in Italia. Ed è anche una questione davvero complessa. La sinistra, quando ha governato, non ha mostrato effettivamente la capacità di affrontare il fenomeno e di dare una risposta soddisfacente alle apprensioni dei comuni cittadini. In merito ai promotori, così spiega Wikipedia: «Il quesito referendario che richiedeva il dimezzamento del numero di anni (da dieci a cinque) di legale soggiorno del cittadino straniero extracomunitario per poter presentare la richiesta di concessione della cittadinanza italiana è stato ideato dal segretario di +Europa, Riccardo Magi, che lo ha depositato in Cassazione il 4 settembre 2024. […] Tra i promotori del referendum, oltre a +Europa, figuravano il Partito della Rifondazione Comunista, il Partito Socialista Italiano, Possibile e i Radicali Italiani, […] numerose associazioni di persone con background migratorio come Italiani senza cittadinanza, il Coordinamento Nazionale Nuove Generazioni Italiane (CoNNGI) e Idem Network, e diverse organizzazioni della società civile, fra cui Libera, A Buon Diritto, Gruppo Abele e ARCI, oltre a varie personalità come Mauro Palma, Luigi Manconi e Ivan Novelli». Nelle intenzioni, dimezzare i tempi per ottenere la cittadinanza avrebbe ottenuto un effetto d’integrazione, evitando di lasciare gli aspiranti in un limbo di incertezza.

Naturalmente, l’ipotesi dei promotori era che l’elettorato – su questa questione – fosse enormemente più maturo del sistema politico nel suo complesso e rispetto ai discutibili provvedimenti sull’emigrazione della attuale maggioranza. Col senno di poi, i risultati del voto hanno invece mostrato la sussistenza di una notevole spaccatura tra gli stessi elettori votanti, una parte consistente dei quali ha indicato il No (34,66%), pur avendo risposto positivamente ai quesiti sul Lavoro. La attuale opposizione sembra dunque fortemente spaccata tra i fautori dei diritti civili e i fautori dei diritti economico sociali.

10. Notevolmente più complessa è la questione della iniziativa referendaria legata ai quesiti sul lavoro. I quattro Referendum sono stati proposti da un Comitato presieduto da Maurizio Landini e comprendente numerosi soggetti: CGIL, Auser, Camere del Lavoro, Libera, Libertà e Giustizia, Federconsumatori, Articolo 21, ARCI, UDU, Rete degli studenti medi, Medicina Democratica, Magistratura democratica, Forum Disuguaglianze e Diversità, Giuristi democratici, USiGRai, FNSI.[3] C’è una storia pregressa che è assai significativa. La lontana origine della questione può essere individuata – anche in questo caso – in una radicale spaccatura nella sinistra determinata dal governo Renzi e dalla sua riforma dei rapporti di lavoro denominata Jobs Act, che risale al 2014-2015. Renzi compì una forzatura, portò con sé la maggioranza nel PD ma determinò sostanziose reazioni di rigetto. Determinerà anche – la cosa riguarda molto da vicino il nostro argomento – la costituzione, da parte dell’allora segretario della FIOM, Maurizio Landini, della cosiddetta Coalizione sociale, che anticipava diversi temi dei Referendum del 2025. Sulla Coalizione sociale di Landini posso rinviare a un mio saggio analitico, scritto nel 2015 e appena rivisto per questa occasione.[4]

La spaccatura indotta dal Jobs Act determinò, nel 2017, la scissione dal PD della formazione che si chiamerà significativamente Articolo 1. Risale poi fin dal 2015 il tentativo di una parte del movimento sindacale di ricorrere al Referendum contro il Jobs Act. Da Wikipedia: «Dopo uno sciopero e numerose manifestazioni contro la riforma del lavoro introdotta dal Jobs Act nel marzo 2014 dal governo Renzi,[…] nel 2016 la CGIL, allora guidata da Susanna Camusso, lanciò una campagna di raccolta firme a favore di un referendum per ripristinare le tutele dell’articolo 18 dello Statuto dei lavoratori per i licenziamenti illegittimi ed estenderle a tutte le aziende con almeno cinque dipendenti: questo articolo, che prevedeva la reintegrazione del lavoratore nel posto di lavoro in caso di licenziamento illegittimo, era stato modificato nel 2015 dal Jobs Act, che invece prevedeva un risarcimento economico.[…] La CGIL riuscì a raccogliere 3,3 milioni di firme in tutta Italia.[…] Tuttavia, l’11 gennaio 2017, la Corte costituzionale dichiarò inammissibile il quesito referendario,[…] poiché era stato erroneamente formulato». Quella del Referendum del 2025 è dunque una storia che viene da lontano, da una radice di scontri e scissioni all’interno del mondo del lavoro e della sinistra stessa.

11. Cardine della analisi di Landini (con assoluta coerenza, dal 2015 a oggi) era ed è la convinzione che la legislazione sul lavoro degli ultimi decenni abbia tolto dei diritti ai lavoratori e abbia prodotto la precarizzazione del lavoro. C’è senz’altro del vero in quel che dice Landini, anche se non possiamo qui entrare nel merito. Secondo Landini le peggiori leggi sul lavoro erano state prodotte dal Governo Renzi, cioè dalla Sinistra al governo, proprio con il Jobs Act del 2015. Di qui l’esigenza di correggere questo andamento, di difendere e ripristinare i diritti dei lavoratori. Ben due dei quattro Referendum sul lavoro riguardano il Jobs Act di Renzi. Si tratta dunque effettivamente di un conflitto interno alla Sinistra, oltre che di un conflitto con l’attuale maggioranza di Governo. Un conflitto che è perfettamente riprodotto dentro all’odierno PD. Per questo la decisione di Elly Schlein di appoggiare tutti e quattro i referendum proposti dalla CGIL è stata considerata come una vera e propria svolta da parte del PD. Anche se i malumori di una parte del PD sono decisamente evidenti.

12. In termini teorici, tuttavia, c’è dell’altro. Siamo in presenza di una analisi ben più generale intorno alle modalità relative alla rappresentanza dei cittadini e dei lavoratori. Landini ritiene che l’attuale sistema politico italiano (non solo la attuale maggioranza!) non abbia rappresentato e non rappresenti adeguatamente i lavoratori. I partiti stessi della sinistra avrebbero tradito gli interessi dei lavoratori. Quindi sarebbe del tutto lecito e giusto mettere in campo un’opposizione contro tutto ciò. Lo slogan ufficiale dei Referendum sul lavoro è «Il voto è la nostra rivolta». Le modalità di questa opposizione vanno appunto dalla “rivolta sociale” cui Landini ha fatto spesso riferimento, alla “coalizione sociale” del 2015/ 2016. Una delle possibilità messe in campo fin dal 2015 era proprio l’uso del referendum abrogativo nei confronti delle norme sul lavoro ritenute maggiormente vessative. Fino all’ipotetico tentativo – ed è questo un motivo ricorrente – di formare un nuovo soggetto politico, un partito del lavoro. Circa la ipotesi di fondazione di un partito politico che avesse come fulcro il mondo del lavoro va ricordato che, in seguito a una scissione del PD di Matteo Renzi, si ebbe la formazione, il 25 febbraio 2017, di Articolo 1 - Movimento Democratico e Progressista, partito politico che venne sciolto il 10 gennaio 2023. Molti degli scissionisti tornarono nel PD. Si tratterebbe dunque di dejà vu. Landini comunque ha recentemente affermato che non intende riprendere l’idea del partito.

13. La ricerca di Landini è comunque sempre andata nella direzione di una rappresentanza alternativa, capace di sostituirsi o contrapporsi alla mancata rappresentanza del lavoro da parte degli ufficiali canali democratici. Come si è visto tuttavia, Landini in questo progetto non è riuscito neppure a trovare l’alleanza delle altre sigle sindacali. La sua è stata una sorta di auto investitura di rappresentanza politica del lavoro, e non semplicemente degli interessi particolari dei lavoratori. L’insuccesso dei quattro Referendum sul lavoro sta mettendo in rilievo un vero e proprio conflitto nell’ambito della rappresentanza. I cittadini italiani, attraverso le loro istituzioni politiche rappresentative, hanno prodotto e producono leggi che precarizzano il lavoro. Allora, quegli stessi cittadini, mobilitati e consultati idealmente in quanto lavoratori, dovrebbero disfare quelle stesse leggi che essi stessi, indirettamente, avevano prodotto come cittadini. A partire dallo slogan «Il voto è la nostra rivolta», saremmo tentati di suggerire che si tratti di una rivolta dei cittadini contro se stessi. Tutto legale, certo, ma per lo meno problematico e bizzarro.

È fuor di dubbio che il rendimento del sistema politico italiano in generale sia catastrofico. Ne ho scritto recentemente.[5] Che con i Referendum abrogativi si possa correggere il basso rendimento della politica italiana è in generale alquanto discutibile. Anche perché dietro si nasconde una tentazione populista. Si tratterebbe di rimettere in sesto il funzionamento della politica. E certo si tratta di una mission pressoché impossible.[6] L’invocazione di una rappresentanza politica alternativa per i lavoratori, rispetto a quella della cittadinanza democratica, implica una dichiarazione di rottura nei confronti delle malferme istituzioni politiche che abbiamo. Implica che ci sia ormai una frattura inemendabile. Nella tradizione del movimento operaio del secolo scorso questa cosa si chiamava conflitto di classe. La ideologia che sostiene la legittimità di una rappresentanza politica dei lavoratori, da far valere anche contro la rappresentanza politica dei cittadini, ha una precisa definizione concettuale: si chiama lavorismo. Se si vuole, in italiano si è parlato spesso anche di operaismo. Il lavorismo è dunque una precisa concezione politica che pare sia stata di fatto adottata dalla CGIL di Landini e che pare stia dietro alla scelta del Referendum. Storicamente, è uno schema d’azione che è definibile come novecentesco. Questo non significa che sia per ciò stesso sbagliato. Si tratta di capire fino in fondo e di valutare quanto sia corretta l’analisi di cui sopra, che dà per scontata, almeno nel nostro Paese, la inefficacia totale della rappresentanza politica e l’impossibilità di porvi rimedio. È una scelta che implica, tra l’altro, oltre alla conflittualità permanente, una condizione minoritaria permanente di chi intende rappresentare il lavoro.

14. E veniamo alle conseguenze. Sul piano delle conseguenze, la sconfitta dei Referendum, dovuta al mancato raggiungimento del quorum, con uno scarto pesante di ben venti punti percentuali, è un fatto assai grave, soprattutto perché dei problemi posti nei quesiti referendari non si parlerà più per un bel po’. E ciò costituisce senz’altro un grave danno in prospettiva per la causa del lavoro e della cittadinanza. Ci saranno probabilmente anche delle conseguenze concernenti l’istituto referendario. Il Referendum è andato soggetto, per l’ennesima volta, a una sorta di stiramento, quando non di snaturamento vero e proprio. Con il rischio di aprire le porte a modifiche estemporanee che non si sa dove potrebbero portare. Si parla di aumentare il numero delle firme necessarie, di un abbassamento del quorum, di introdurre il referendum propositivo. Con tutti gli ingegneri costituzionali che abbiamo, c’è il serio rischio di decisioni avventate che potrebbero anche peggiorare le cose. L’uso dell’astensione, fatto spregiudicatamente e perigliosamente dai sostenitori del No, ha poi finito oltretutto per confondersi con la pericolosa tendenza all’astensionismo elettorale che si registra da tempo nel nostro Paese, e che sta mettendo a repentaglio la nostra stessa democrazia.

15. Ma veniamo ora a costatare alcune conseguenze più specifiche. Il Referendum intanto ha costituito l’ennesima occasione per celebrare la disunità sindacale nel nostro Paese. Mentre la CGIL ha dato ovviamente l’indicazione di votare Sì ai cinque quesiti, la CISL ha indicato nientemeno che l’astensione generalizzata, mirando così al mancato raggiungimento del quorum e alla invalidazione della consultazione. Il secondo sindacato italiano, per numero di aderenti si è schierato dunque nettamente contro la teoria della rappresentanza del lavoro di Landini. La UIL ha dato l’indicazione di votare Sì al Reintegro e ai Subappalti e ha lasciato libertà per gli altri quesiti, considerando quindi come opinabili i tre quesiti sulla Indennità, i Contratti a termine e la Cittadinanza. Cose non da poco. In generale, la decisione della CISL pare proprio abbia messo la pietra tombale sull’unità sindacale. Se è senz’altro vero che certe leggi recenti hanno danneggiato i lavoratori, è senz’altro vero che un danno ancor più grande è stato fatto loro proprio dalla disunità sindacale.

16. Il Referendum ha messo in luce anche la disunità politica della opposizione, il cosiddetto campo largo, e ha anche segnato notevoli disparità di opinioni all’interno del PD, il principale partito di opposizione. Il M5S ha dato indicazione di votare Sì per i quattro quesiti sul lavoro e ha lasciato libertà per Cittadinanza. Italia Viva ha dato indicazione di votare No ai quesiti sul lavoro, lasciando tuttavia libertà per Indennità e Subappalti, e di votare Sì alla Cittadinanza. Azione di Calenda ha proposto quattro No ai quesiti sul lavoro e Sì a quello sulla Cittadinanza. AVS di Bonelli e Fratoianni ha proposto cinque Sì. Più Europa ha proposto No a Reintegro, Indennità e Contratto a termine e Sì per Subappalti e Cittadinanza. I Radicali hanno dato indicazione di votare No ai Referendum sul lavoro e sì a Cittadinanza. Un pluralismo davvero straordinario! Che cento fiori fioriscano, che cento scuole gareggino!

Il fatto che le formazioni dell’opposizione, candidate alla costituzione del cosiddetto campo largo, abbiano manifestato posizioni così contrastanti su questioni così cardinali come il lavoro e la cittadinanza è indicativo del profondo malessere dell’opposizione. In termini di previsione, possiamo dire che nelle elezioni politiche nazionali che si terranno – presumibilmente – nel 2027 le prospettive di vittoria della sinistra siano prossime pressoché allo zero.

Va detto, in margine a queste giravolte, che la campagna elettorale è stata quasi priva di dibattito, tra le diverse forze politiche e sindacali, e l’onere della mobilitazione – invero assai generosa – è caduto di fatto sulla CGIL e pochi altri. Ovviamente le centrali della disinformazione hanno fatto il loro mestiere. Come al solito si sono sentite, da parte dei sostenitori del Sì, aspre recriminazioni nei confronti della informazione e soprattutto del Servizio pubblico televisivo. Fino a sostenere che il Sì avrebbe perso a causa del boicottaggio dell’informazione. L’ipotesi ci pare un tantino esagerata, anche se un qualche fondamento ce l’ha.

17. E, per finire, uno sguardo sui destinatari dei Referendum. Quando si perde, sorge spontanea la tentazione di colpevolizzare gli elettori. Questa tendenza si mescola volentieri con le interpretazioni o con le spiegazioni. Elettori cattivi cittadini che hanno preferito “andare al mare”, oppure che hanno obbedito al consiglio di “andare al mare” da parte degli astensionisti. Elettori poco informati dai media. O elettori distratti. Elettori che hanno ceduto alla politicizzazione del discorso referendario e quindi, invece di entrare nel merito delle questioni, hanno seguito i consigli della loro parte politica. Elettori che hanno ritenuto che gli argomenti specifici dei cinque Referendum non li riguardassero direttamente. Elettori che hanno desistito per repulsione nei confronti degli immigrati – per cui la colpa del basso afflusso ai seggi sarebbe stata dovuta, secondo taluni, alla presenza del quinto Referendum. Se ne potrebbero citare altre ancora.

18. Ho sentito Landini affermare con grande convinzione che si trattava di convincere ad andare a votare gli astenuti (alle elezioni politiche). Beata speranza. È questo il sogno eterno della sinistra che dentro/ dietro gli astenuti del voto ci sia un grande potenziale di protesta. Dal mio punto di vista, questa è una prospettiva che sta fuori dal mondo. Gli astenuti, purtroppo, sono cittadini deteriorati, cittadini perduti. Sono la feccia della cittadinanza. Sono in gran parte irrecuperabili, carne da macello mobilitabile solo dal populismo becero. Sono la conseguenza della sparizione progressiva della cultura civica repubblicana e democratica dal nostro Paese. E anche questa sparizione ha le sue cause ben precise. Non entro nel merito per brevità. La narrazione circa il potenziale di protesta degli astenuti si basa sul mito dei cittadini buoni e delle istituzioni cattive. Gli astenuti si sentono messi da parte dalle cattive istituzioni, non vanno a votare per protesta ma conservano un istinto certo circa i loro autentici interessi: se proponi loro qualcosa di conveniente (vedi i motivi assai concreti dei quattro referendum) questi non potranno che rispondere positivamente! Non sembra proprio sia andata così.

19. Nel ragionamento di Landini si vede all’opera, forse inconsapevolmente, l’economicismo che è stato tipico da sempre della sinistra. L’elettore considerato come homo oeconomicus. Ebbene, questa visione è smentita dai risultati. La maggior parte degli elettori (cittadini e lavoratori) non ha ritenuto rientrassero nel proprio interesse una serie di vantaggi elementari, come il Reintegro, l’Indennità, i Contratti a termine e i Subappalti. Come mai? Hanno avuto ragione o si sono sbagliati?

C’è innanzitutto da considerare un dato statistico; da noi il lavoro dipendente contrattualizzato o contrattualizzato a termine (tale da rientrare nelle fattispecie di rischio e precarietà previste dai Referendum) è una minoranza rispetto ai 51 301 377 di aventi diritto al voto, sui quali si calcola il quorum. E poi non dappertutto ci sono cose come i subappalti. Anzi, questi sono caratteristici solo di taluni settori. Molti lavori addirittura sono in nero o non contrattualizzati. Poi abbiamo l’economia degli schiavi.[7] Ma ci sono anche gli ultra garantiti che hanno il posto fisso, dove le probabilità di essere licenziati o di cadere da un’impalcatura sono altrettanto minime. Si consideri poi l’intero pubblico impiego, non coinvolto. Ma ci sono anche le partite IVA che cadono fuori dal discorso, oppure gli ultra professionalizzati che, se perdono il lavoro, devono solo alzar mano per trovarne subito un altro. Poi c’è la valanga di coloro che sono in pensione, certo poco interessati al mondo del lavoro. Insomma, i quattro referendum si rivolgono a uno specifico tipo ideale di lavoratore, sottoposto a rischio e precarietà, effettivamente danneggiato dal Jobs Act e dalle altre disposizioni sul lavoro. Un tipo di lavoratore per il quale potrebbe avere effettivamente senso una battaglia per recuperare uno straccio di dignità, come sostiene Landini.

20. Quanti sono costoro? Se non fosse un lavoraccio (ahimè nessuno mi paga!), sarebbe utile, a partire dai dati statistici, fare una stima del numero dei possibili diretti destinatari dei provvedimenti referendari. Per brevità, tanto per dare un’idea approssimativa dell’entità di questo “popolo”, userò la tabella sintetica recentemente pubblicata da Pier Giorgio Ardeni[8], che è relativa a dati del 2023. Com’è noto, Ardeni segue lo schema delle classi sociali proposto da Paolo Sylos Labini. Gli occupati complessivi, relativi a tutte le classi sociali, risultavano 23 647 390. Di questi, coloro che sono qualificabili come classe operaia ammontano a 5 528 599. Questi comprendono salariati agricoli (340 317), salariati dell’industria (2 630 698), salariati dell’edilizia (716 230), salariati del commercio (511 603) e salariati di trasporti e servizi (1 329 751). A questi 5,5 milioni andrebbero aggiunti – se comprendiamo bene la tabella di Ardeni – gli impiegati e i dipendenti privati, classificati sotto “piccola borghesia impiegatizia” e che ammontano a 8 241 009. Non vanno inclusi gli impiegati pubblici, cui non si applicano le tematiche referendarie.

Il target dei direttamente interessati dunque, in senso stretto ammonterebbe ai 5 milioni e mezzo, cioè i classificati come classe operaia. Se aggiungiamo a costoro gli impiegati e i dipendenti privati (per i quali tuttavia la condizione di rischio e precarietà senz’altro meno impellente) possiamo allargare la cifra fino a 13 769 608. Ricordo che il quorum per il Referendum 2025 ammontava a 25 650 689. Anche solo ragionando in termini di interesse individuale, anche pensando che ognuno di costoro avesse un parente che vota per lui, l’impresa del quorum era piuttosto in salita.

21. I quattro Referendum, nella loro specificità tematica, sembrano tendere a ridurre piuttosto che ad ampliare la platea dei diretti interessati. Allora bisogna riconoscere che la fattispecie dei destinatari dei quattro referendum sul lavoro corrisponde a un tipo ideale di lavoratore – perfettamente coerente con una certa ideologia del lavoro, quella che abbiamo chiamato lavorismo – che tuttavia è ben lungi dal corrispondere all’intero universo statistico dei lavoratori in generale. Non sto dicendo che la fattispecie di rischio e precarietà individuata dai quattro Referendum non esista. Esiste eccome e probabilmente è anche in aumento. Ma questa è solo una delle multiformi facce del lavoro odierno. Non dappertutto ci sono subappalti o contratti a termine. I promotori dei quattro Referendum sul lavoro hanno preso una casistica specifica, senz’altro moralmente e politicamente degna di ogni attenzione, senz’altro di grande valore simbolico, e l’hanno estesa a tutto il mondo del lavoro. Perché? Qui si potrebbero sprecare i riferimenti storici. Si ricordi il proletariato tedesco di Marx che da classe particolare diventava classe generale, tanto da liberare l’intera umanità dall’alienazione. Tempo fa scrissi un ampio saggio su questo argomento.[9] Ebbene, l’ampio mondo del lavoro e l’ancor più ampio elettorato sembra non si sia riconosciuto più di tanto nel tipo ideale di lavoratore emergente dai quesiti referendari.

22. Ma c’è un altro fatto più generale da considerare, che prescinde dall’homo oeconomicus e che anzi lo rende decisamente meno importante di quanto non si creda comunemente. Il fatto è che l’elettore medio odierno è assolutamente incapace anche solo di fare un calcolo oggettivo dei propri interessi che vada oltre l’immediato. Per avere un atteggiamento realistico verso il mondo, per essere in grado di fare un calcolo non distorto dei propri interessi, occorrerebbe un elettore lucido, correttamente informato, liberato da tutta la fuffa accumulata nel proprio cervello dai social media e dalla comunicazione populista. La sovrastruttura mediatica imperante, che ha preso il posto dell’opinione pubblica, impedisce sistematicamente all’elettore medio di fare il calcolo dei propri effettivi interessi. Landini dice all’elettore medio «Vota per me, nel tuo interesse!». Ma l’elettore medio è così internamente strutturato che quell’interesse proprio non lo vede, non può vederlo. Non nell’immediato e neanche in prospettiva. È purtroppo finita l’epoca dei calcolatores. L’epoca della rational choice.[10] L’elettore medio sceglie sulla base del “noi”, di quelli che più ritiene gli somiglino, sotto i profili più vari. È istintivamente identitario! E chiunque, per la sua preziosa identità, sarebbe disposto a scordare anche i propri interessi immediati. Ho trattato diffusamente di questo tipo umano nel mio recente saggio sulle elezioni americane.[11]

23. Sembra che non abbiamo imparato proprio niente da Berlusconi e da Trump. Le famose casalinghe votavano per Berlusconi, il quale aveva un profondo disprezzo per le donne. Gli americani poveri, magari per una legittima antipatia verso i democratici delle due Coste, hanno votato per un uomo ultra ricco che disprezza i poveri e li usa per i suoi interessi di parte e tornaconti personali. È, questo, esattamente un atteggiamento di pancia, come quello che consigliava Grillo, alla lettera, qualche tempo fa ai suoi seguaci. Non a caso, i Referendum di Landini sono andati meglio nei soliti posti, tipo ZTL, tra i laureati e gli antipatici intellettuali. Si tratta tuttavia ahimè di una minoranza. Purtroppo la laurea è ancora soggetta a qualche restrizione, anche se ben presto la regaleremo proprio a tutti. Ma allora sarà cosi squalificata che non farà più alcuna differenza.

Giuseppe Rinaldi  (11/06/2025)

 

OPERE CITATE

2024 Ardeni, Pier Giorgio, Le classi sociali in Italia oggi, Laterza, Bari.

2019 Ricolfi, Luca, La società signorile di massa, La nave di Teseo, Milano.

 

 

NOTE

[1] Sull’argomento trattato in questo saggio ho potuto beneficiare di uno scambio di idee, aperto e partecipato, con gli amici di Città Futura, che ringrazio sentitamente. Ovviamente la responsabilità di quanto qui vien sostenuto è esclusivamente mia. Preciso che nella redazione di questo saggio non ho fatto uso di alcuno strumento di intelligenza artificiale. Nel corso di questo scritto, adotterò le seguenti abbreviazioni per indicare i diversi Referendum: Reintegro, Indennità, Contratto a termine, Subappalti, Cittadinanza.

[2] Fonte Wikipedia.

[3] Fonte Wikipedia.

[4] Rinvio al mio saggio del 2015 Dal sociale non nasce niente che rappresentava un tentativo di analisi della Coalizione sociale, di cui all’epoca si discuteva alquanto. Cfr. Finestre rotte: Dal sociale non nasce niente .

[5] Cfr. il mio recente saggio: Finestre rotte: Finestre rotte: Toh, chi si rivede. Etica e politica! Soprattutto l’ultima parte.

[6] Si tratterebbe di capire perché, nella storia recente del nostro Paese, si siano fatti innumerevoli tentativi, almeno da Tangentopoli in poi, per riformare il sistema politico complessivo. Tentativi che non hanno risolto nulla. L’Autonomia differenziata e il Premierato di Calderoli/ Meloni sono solo l’ennesima favola che promette il rinnovamento della politica. Dati i trascorsi conflittuali del passato e del presente, la sinistra, nel suo complesso, sembra avere totalmente rinunciato all’obiettivo in questione e sembra essersi totalmente rassegnata alla politica inconcludente.

[7] Si veda il saggio di Luca Ricolfi La società signorile di massa. Cfr. Ricolfi 2019.

[8] Cfr. Ardeni 2024.

[9] Si veda in proposito il mio saggio storico filosofico, sempre del 2015, Classe generale e interessi particolari. Cfr. Finestre rotte: Classe generale e interessi particolari.

[10] Come studioso di scienze sociali sono affranto. Tutti i valorosi modelli economici e sociologici basati sulla rational choice sono sempre più destituiti di fondamento! Ormai le idee distorte che stanno nella testa di ciascuno sopravanzano completamente gli interessi oggettivi, per cui ogni previsione nel mondo sociale è sempre più difficile.

[11] Chi è interessato a queste tematiche può approfondire il concetto di mutazione antropologica, che ho usato per interpretare il comportamento degli elettori americani che hanno votato per Trump contro i loro stessi interessi. Cfr. Finestre rotte: Le elezioni americane e noi .

 

 

 

 

.